他にも自分で試してみると面白いと思います。$r_1=1$、$r_2=3$ とするとどうなるでしょうか。同じように、計算と図をかいてみましょう。さらに片方の出口を大きくしていくと、どうなっていくでしょうか。
実際の血管を観察した研究によると、2乗でも4乗でもなく、3乗に近い値であることが分かっています。私たちの体に、$r_0^{\,3}=r_1^{\,3}+r_2^{\,3}$ という「三立方の定理」が隠れていて、生命を維持してくれていると考えると面白いかもしれませんね。
数学で困ったときは、このように具体的な数で地道に考えてみると分かることがあります。最初から文字式の計算だけで(本当の意味で)理解できる人は少ないです。初めて3乗則の式 $r_0^{\,3}=r_1^{\,3}+r_2^{\,3}$ だけを見たときと、具体例を扱った今、理解度が違うのではないでしょうか。
公式はすぐに役立ちますが、忘れてすぐに役立たなくなります。公式暗記を繰り返して(定期テストで一瞬点は取れるものの、模試では)成績がなかなか上がらない…そんな経験がある人も多いのではないでしょうか。
一方で、数の代入実験で得られた経験は、地道で少し手間?はかかるものの、忘れにくく、身になります。体験って大切です。同じような「考え方」を応用できるメリットもあります。ぜひ、意識してやってみてください。
エネルギーを最小に
半径 $r$、長さ $\ell$ の血管を考えましょう。この血管内を流れる流量を $f$ とします(単位時間当たりの血液の体積)。
血管で消費されるエネルギーは血液を流すためのエネルギー(機械的エネルギー)と血液を新鮮に保つためのエネルギー(化学的エネルギー)のふたつがあります。 このふたつのエネルギーの和 $E$ を考えて、これを最小にする構造を最適なものと考えます。
$E=$(流すエネルギー)$+$(保つエネルギー)
長さ $\ell$ と流量 $f$ を一定にして、半径 $r$ を変化させてみます。
流すエネルギー:血液の粘度の高さから、半径 $r$ が小さいと、摩擦抵抗が高くなります。同じ流量 $f$ を流すためには、流速を上げて流すエネルギーを大きくする必要があります。逆に、半径 $r$ が大きくなると、摩擦抵抗が小さくなり、流すエネルギーも小さくなります。反比例のような関係ですね。
保つエネルギー:血液を新鮮で活動的に保っておくためにエネルギーが必要です。血液の量が多いほど維持が大変ですので、エネルギーは血液量に比例すると考えられます。単純に、半径 $r$ が大きいときは、血液も多く、保つエネルギーは大きくなります。半径 $r$ が小さいときは、血液は少なく、保つエネルギーは小さくなります。
血液を流すためのエネルギーと血液を保つためのエネルギーの和 $E$ が、半径がどのようなとき最小になるかを計算で導きます。
エネルギーを半径の式で
それぞれのエネルギーを半径 $r$ の式で表すことを考えます。
保つエネルギー:計算が簡単な方の保つエネルギーから。血液量 $V$ に比例することから、比例定数を $k$ とすれば、(保つエネルギー)$=kV$ となります。体積は $V=$(底面積)$\times$(高さ)$=\pi r^2\times \ell$ ですので、
(保つエネルギー)$=\ kV=k\pi r^2\ell$
となります。半径 $r$ の式で表すことができました。ちゃんと半径 $r$ を大きくするとエネルギーが大きくなる式になっていますね。
流すエネルギー:続いて、流すエネルギーは、血管の入口と出口の圧力差と血液の流量の掛け算になります。
(流すエネルギー)$=$(圧力差)$\times$(血液流量)$=$ $\Delta p\times f$
$\Delta p$ は圧力差を表します。デルタ $\Delta$ は Differrence(差)のDで、$\Delta p$ は $p$ の差と読めばOKです。上の式は、圧力差があるほど、流量が多いほど、血液を流すエネルギーが必要だ、と読めます。
ハーゲン・ポアズイユの法則:流量 $f$ と半径 $r$ には次のような関係があります(本学では3年次の実験で登場)。
流量 $f=\dfrac{\pi}{\,8\mu\,}\dfrac{\,\Delta p\,}{\ell}\,r^4$
なんだか難しそう!と思うかもしれませんが、ひとつひとつ見ていけば大丈夫です。$\mu$ はねばねば具合(粘性係数)です。ねばねば具合が大きくなると、分母が大きくなって、流量 $f$ が小さくなります。ねばねばすると流れにくい、と読んでおけば良いでしょう。$\pi/8\mu$ は定数ですので、今はあまり気にしなくて良いです。
大事なところは、流量 $f$ が半径 $r$ の4乗に比例していることです。半径が大きくなると流量は多くなる訳ですが、4乗に比例するということは、たとえば、半径が2倍になると2の4乗で流量は16倍になるということです。半径が2倍なら流量も2倍どころか、16倍にも増えるのですね。
ハーゲン・ポアズイユの式を $\Delta p$ について解いて、代入すると次のようになります。
(流すエネルギー)$=\Delta p\times f=\dfrac{\,8\mu f^2\ell\,}{\pi r^4}$
以上より、エネルギーの和は
$E=\dfrac{\,8\mu f^2\ell\,}{\pi r^4}+k\pi r^2 \ell$
となります。文字は多いですが、半径 $r$ に注目すれば、$1/r^4+r^2$ の形になっています。
半径がいくつのときエネルギーの和が最小に?(少し計算あり)
あとは、半径がいくつのとき、エネルギーの和 $E$ が最小になるかです。ここで微分の出番です。山の谷のように最小になるときは、グラフの接線の傾きはゼロになります。微分によって接線の傾きを求めることができますので、微分 $=0$ を解けば何か結論が出るはずです。グラフがかける人はかいてみると理解が深まるでしょう。
計算してみると、$f=c\times r^3$ という関係式が導かれます($c$ は定数)。
少し復習:微分は傾きです。たとえば、$y=2x$ を微分すると $y^{\prime}=2$ です。変に公式を使うのではなく、これは「直線 $y=2x$ の傾きは $2$ です(1進むと、2上がる)」と答えただけの話と考えましょう。
直線以外になると計算する必要はありますが、定数乗の場合は、$(x^2)^{\prime}=2x$、$(x^3)^{\prime}=3x^2$ と同様にできます。たとえは、$1/x^2$ の微分は $1/2x$ ではなく、$1/x^2=x^{-2}$ として、$(1/x^2)^{\prime}=(x^{-2})^{\prime}=-2x^{-2-1}=-2/x^3$ となります。
エネルギーの和は $E=\frac{\,8\mu f^2\ell\,}{\pi}\,r^{-4}+k\pi \ell \,r^2 $ と書けるので、微分すると
$\dfrac{\,dE\,}{dr}=\dfrac{\,8\mu f^2\ell\,}{\pi}\,(-4r^{-4-1})+k\pi \ell \cdot 2r $
となります。$dE/dr$ は$E$ を $r$ で微分するという意味です($r$ を変化させたとき、どのくらい $E$ が変かするか?)。難しく考えずに、$E^{\prime}$ と思って問題ありません。
ここで、$\dfrac{\,dE\,}{dr}=0$(傾きがゼロ)としてみましょう。$f$ と $r$ に注目して整理していくと、$\dfrac{\,f^2\,}{r^6}=\dfrac{\,k\pi^2\,}{16\mu}$ となります(少し紙で計算してみましょう)。これから、$\dfrac{f}{\,r^3\,}=\dfrac{\,\pi\,}{4}\sqrt{\dfrac{k}{\,\mu\,}}$(一定)が得られます。書き換えることで、$f=c\times r^3$ が得られます(定数部分を $c$ とおきました)。
「血管の3乗則」まであと一歩!
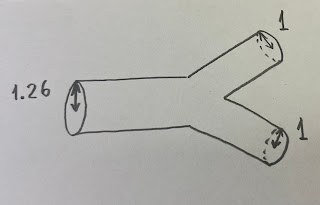
入口の流量を $f_0$、分岐した出口の流量を $f_1$、$f_2$ とします。入口と出口の流量は同じはずですので、
$f_0=f_1+f_2$
が成り立つことが分かると思います。上の計算結果から、$f_0=c\,r_0^{\,3}$、$f_1=c\,r_1^{\,3}$、$f_2=c\,r_2^{\,3}$ となります(定数 $c$ は同じ!)。これを代入すれば、
$c\,r_0^{\,3}=c\,r_1^{\,3}+c\,r_2^{\,3}$
両辺 $c$ で割って、
$r_0^{\,3}=r_1^{\,3}+r_2^{\,3}$
これで「血管の3乗則」が得られました。流量 $f$ を半径 $r$ の式に表すことさえできれば、あとは $f_0=f_1+f_2$ から出てくる訳ですね。
全体を良く見返してみると、流すエネルギーの4乗と保つエネルギーの2乗が効いて、3乗が出てきています。今回は半径に注目しましたが、分岐の角度についても考察ができたりします。
血管の「カタチ」に興味がある人は、文献・ネットを調べてみたり、下記の参考書に当たってみると良いでしょう。
【参考書】
- 伊能教夫『生物機械工学:数理モデルで生物の不思議に迫る』コロナ社(第4章:血管の分岐)














%20(2).jpg)
%20(1).jpg)



%20(1).jpg)

%20(2).JPG)


.png)


.png)


.png)





